1.현대물리학-RELATIVITY I
RELATIVITY I
1.1 특수 상대성 이론 개요
1905년 26살의 아인슈타인은 ‘special theory of relativity’라는 제목의 논문을 출판했다. 아인슈타인의 논문에 따르면 다음과 같다.
‘상대론은 탈출구가 없는 예전 이론의 심각한 모순으로부터 태어났다. 몇 개의 가정에 확신을 가진다면 이 새로운 이론은 일관적이고 간단명료하여 모든 어려움을 해결할 수 있다.’
일상에서 물체들은 경험상 빛의 속도보다 훨씬 작은 속도로 움직인다. 뉴턴역학은 느린 속도계에서 잘 적용되었지만 빛의 속도에 근접하게 움직이는 물체에는 적용할 수 없었다.
실험적으로 높은 전위차에서 전자가 높은 속도로 가속될 때 뉴턴 역학을 테스트해볼 수 있다. 수백만 볼트의 전위차에서 전자를 0.99c 속력에 가깝게 가속시킨다고 가정해보자. 만약 전위차가 4배 증가하면 전자의 속력은 두배인 1.98c가 된다. 하지만 모든 실험들은 voltage를 아무리 증가시켜도 전자뿐만 아니라 모든 입자들의 속도는 항상 빛의 속도 이하이다. 따라서 뉴턴 역학은 한계가 존재하는 이론이다.
우리는 일정한 속력을 가지고 직선으로 움직이는 서로 다른 물체가 좌표계에서 어떻게 물리적으로 분석되는지 살펴보고, 더 나아가 가속 좌표계에서 일반화하여 물리적 현상을 설명할 수 있는 일반 상대론의 기초를 알아볼 것이다.
1.2.1 상대성의 법칙
물리 현상을 설명하기 위해서는 항상 하나의 좌표계가 필요하다.뉴턴의 상대성원리에 따르면 역학 법칙은 전부 관성 좌표계에서 똑같이 성립해야 한다.
예를 들어 만약 등속 운동하는 트럭에서 공을 지면과 수직으로 손에서 던지면 다시 손으로 돌아와야 한다. 이때 트럭에서 관측한 사건이 걸리는 시간과 트럭 외부에서 측정한 시간은 같다. 그리고 시간 계산을 위해 동일한 뉴턴의 제2법칙 ($F = ma$) 이 사용된다. 동일한 실험이 관측자에 따라 다른 궤적과 속도를 가지지만 두 관측자 모두 뉴턴 법칙이 성립하고 에너지와 운동량이 보존된다는 것에 동의할 것이다.
이는 역학 실험이 두 관성 좌표계의 차이를 보여줄 수 없다는 것을 의미한다. 오직 증명할 수 있는 것은 한 좌표계에 대한 다른 좌표계의 상대적인 운동뿐이다. 즉, space에서 absolute motion 개념은 의미가 없다. Absolute motion은 절대적인 기준이 되는 관성 좌표계가 존재함을 의미하기 때문이다.
실제로 현대 과학의 견고한 철학적 원칙 중에 하나는 모든 관측자에 대해 자연의 법칙은 같은 수학적 방법으로 기술된다는 것이다.
첨언
모든 좌표계에서 동일한 수학적 방법으로 설명할 수 있다는 물리학 법칙의 성질을 covariant라고 한다. 보통 general covariance 라고 하며 쉽게 말해, 좌표는 인간이 자연을 이해하기 위해 임의로 설정한 인공물이기 때문에 물리 법칙을 공식화하는 데에 영향을 주어서는 안 된다는 것이다.
수학적 방법론의 측면에서 뉴턴 역학과 상대론의 차이는 텐서이다. 텐서는 선형대수적 측면에서 행렬의 형태로 선형 관계를 다루는 다중선형대수학의 대상 중 하나라고 할 수 있다.
뉴턴 역학에서 시간은 절대적이라고 가정하기 때문에 3차원 직교 좌표계(3 x 3 행렬)로 모든 운동을 설명할 수 있지만 상대론에서는 시간도 하나의 성분으로서 다루기 위해 텐서가 필요하다. 쉽게 말해, frame 속에 시간축이 존재하는 것이다.
다시 covariant에 대한 문장 첫 부분에 있는 ‘모든 좌표계’라는 것은 coordinate system 이 아니라 하나의 시공간적 frame임을 의미한다. 즉, 시간 t 가 포함되어 있는 텐서로 구성된 모든 frame에서 동일한 물리 법칙이 성립함을 얘기하는 것이다.
이 frame에서 에너지와 운동량 보존 법칙에 근거하여 물리 법칙을 공식화했을 때 일반 상대성 이론이 탄생하는 것이다. 수리물리학적인 관점에서 covariant는 물리 세계에 어떠한 형태로 나타나는 것인지 계속 생각해야한다.
단순히 철학적인 이야기는 아니다. 일단 covariant를 설명할 수 있는 도구로 spacetime frame이 있다는 것만 알아두면 된다.
그리고 Noether’s theorem을 고전역학에서 라그랑지안 형태로 증명해봤을 것이다. Noether’s theorem은 ‘하나의 보존법칙은 어떤 미분가능한 물리계의 대칭성과 대응된다’는 것이다. 물리 세계에서 운동량과 에너지 보존법칙은 어떤 대칭성과 대응된다. 이러한 대칭성은 frame에서 회전 대칭, 병진 대칭 등의 형태로 서술할 수 있다. 간단히 말해서, 좌표계에서 원뿔을 주축으로 회전시켜도 같은 상태인 회전 대칭성을 가지고, 일정한 주기를 가지는 파동은 주기 대칭성을 가진다. 이러한 대칭성은 frame에서 수학적으로 기술할 수 있고 대칭성은 보존법칙의 존재성과 대응되니 물리학의 covariant를 설명할 수 있다.
Frame $\iff$ Symmetry $\iff$ Conservation Law $\iff$ Physics $\iff$ Covariant
따라서 물리학자들은 관습적으로 대칭성이라고 부른다.
1.2.2 상대성의 법칙
트럭 실험을 측정할 때, 한 좌표계에서 수행된 측정을 다른 좌표계의 측정과 연결하는 공식이 필요하다. 이를 transformation이라고 하며 뉴턴의 상대성을 만족하는 transformation을 ‘Galilean transformation’이라고 한다.
일정한 속도로 움직이는 두 개의 프레임을 S와 S’이라고 하자. S에서 측정한 S’의 x축 방향의 속력을 v라고 하면 다음과 같은 등식이 성립한다.
$x’ = x – vt$
$y’ = y$
$z’ = z$
$t’ = t$
‘Galilean transformation of coordinates’
4번째 등식은 두 관성 좌표계에서 시간은 동일하게 흐른다는 것을 말한다. 고전역학에서 모든 시간은 속도와 상관없이 동일하게 흐른다.
따라서 하나의 사건에 대해 동일한 시간 간격을 가진다.
$t’ = t \to dt’ = dt$를 이용하여 1번째 등식을 t에 대해 미분하면
$u_x’ = u_x – v$가 성립한다. 이를 ‘Galilean velocity transformation’이라고 한다.
우리가 알고 있는 갈릴레이의 상대속도 개념이다.
이제 한 번 더 t에 대해 미분하면 v가 상수이기 때문에 $a_x’ = a_x$이다.
따라서 다른 관성 좌표계에 있는 관측자는 동일한 실험을 관측할 때 동일한 가속도 값을 측정한다. 이는 가속도와 시간 간격이 불변이라는 것을 의미한다. 따라서 x축에 대해 뉴턴 제2법칙($F=ma$)은 Galilean transformation에서 covariant하다라고 할 수 있다.
그렇다면 운동량 보존에 대해서도 covariant하다고 할 수 있을까. Galilean velocity transformation으로 간단히 증명할 수 있다.
뉴턴의 상대론은 전자기 및 광학에도 적용된다. 1860년대 Maxwell은 진공에서 빛의 속력이 $c = \sqrt{\mu_0\epsilon_0} = 3.0\times10^8 m/s$임을 보였다. (자세한 내용은 전자기학 참고바람)
1800년대 후반 물리학자들은 음파나 물결파처럼 광파도 에테르라는 매질을 통해 전파된다고 확신했다. 빛의 속력이 c인 이유는 에테르가 c의 속력으로 움직이기 때문이라고 생각했고 그것을 에테르 frame이라고 하였다.
에테르 frame에 대해 v의 속도로 움직이는 frame이 있다고 했을 때 같은 방향으로 움직이면 $c – v$의 상대속도를 갖고 반대 방향으로 움직이면 $c + v$의 상대속도를 갖는다고 여겼다. 따라서 빛의 속력은 상대적이며 frame이 움직이는 방향에 따라 상대속도가 달라진다고 생각했다.
그러므로 특별한 에테르 frame의 존재를 확립하는 것이 상당히 중요한 이슈였다. 빛의 속력은 매우 컸기 때문에 1800년대 후반 매질을 통한 빛의 전파를 관측하는 실험에서 $c \pm v$와 같은 작은 변화를 감지해낼 수 없었다.
그 당시에 과학자들은 지구가 태양 주위를 공전하는 속도가 약 30 km/s라는 것을 깨달았고 지구 자체를 움직이는 좌표계로 사용하여 빛의 속력에서 작은 변화를 감지해내기 위한 수단으로 사용하고자 하였다.
지구에 고정되어 있는 관측자인 우리를 기준으로 삼아, 우리 주위를 특별한 에테르 frame이 v라는 속도로 지나가고 있다고 가정했다. 이러한 가정하에 빛의 속력은 공기가 특정 방향으로 흐르는 공간의 바람과 같이 측정할 수 있었다. 우리는 이를 ‘Ether wind’라고 부른다. 만약 지구에 대한 에테르의 상대속도가 v라면, 빛의 속력의 최대값은 $c + v$이고, 최소값은 $c - v$여야 한다. 태양이 에테르 frame에 대해 정지해 있다고 가정하면 에테르 wind의 속도는 지구의 공전속도 v와 같을 것이다. $v = 3\times10^4 m/s $이므로 빛의 속력의 변화는 $1/10^4$ 정확도로 감지할 수 있어야 한다. 하지만 다음 실험에서 볼 수 있듯이 모든 실험은 초기 가정과 모순되었다.
1.3 마이컬슨-몰리 실험
빛의 속력의 작은 변화를 감지하기 위한 시행된 가장 유명한 실험은 1887년에 미국의 물리학자 Albert A. Michelson과 미국의 화학자 Edward W. Morley가 행한 마이컬슨-몰리 실험이다. 이 실험은 고도의 정확한 실험 장비인 마이컬슨 간섭계로 수행되었다. 간섭계의 Arm 중 하나는 지구가 움직이는 방향과 평행하게 놓았고 이는 에테르가 정면에서 불어오는 방향이다. 따라서 빛의 속력은 $c - v$가 되어야 하며 거울에 반사된 빛의 속력은 $c + v$가 되어야 한다. Beam Splitter에 의해 빛은 정방향의 빛과 90도 방향의 빛으로 갈라지게 되고 수직으로 갈라진 빛의 속력은 $\sqrt{c^2 – v^2}$ 이다.
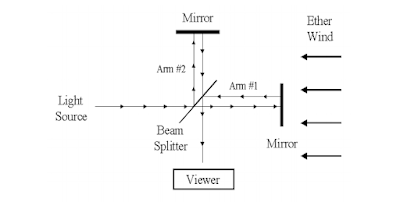
결국 이렇게 만들어진 속도차로 인해 detector로 들어가기 전에 중첩되어 간섭무늬를 만들게 된다. 하지만 이 실험은 이러한 간섭무늬를 만드는데 실패하였다. 다른 연구자들이 이 실험을 다양한 조건하에서 반복해봤지만 절대 fringe shift가 나타나지 않았다.
이러한 마이컬슨-몰리 실험의 결과는 빛의 속력이 전파 방향과 상관없다는 것을 증명할 뿐만 아니라 에테르 가설도 완전히 틀렸음을 밝혀냈다.
마이컬슨-몰리 실험을 더 자세히 살펴보자. 위와 같은 간섭계에서 Splitter에서 동시에 나눠진 빛은 다른 Arm을 거치는데, 이때 ‘Ether wind’에 따른 진행속도가 다르기 때문에 걸리는 시간도 달라지게 된다. 따라서 시간차이는 다른 경로를 거친 파동에 위상차이가 발생한다. 위상차는 간섭무늬를 만들게 되고 간섭무늬의 간격을 계산해 볼 수 있다. 경로길이 $L = 5.5m$이고 지구의 속력 v는 $30km/s$를 넣어 계산하면 다음과 같다.
$ \Delta d = \frac{2(11m)(3\times10^4 m/s)^2}{(3\times10^8 m/s)^2} = 2.2 \times 10^{-7} m $
파장이 약 $500nm$인 빛을 사용하면 Shift되는 비율은 다음과 같다.
$ Shift = \frac{2.2 \times 10^{-7} m}{5.0 \times 10^{-7} m} = 0.40 $
마이컬슨과 몰리가 고안해낸 이 간섭계 실험기구는 간섭무늬 간격의 1%까지 정밀하게 측정할 수 있지만 어떠한 Shift도 감지하지 못했다. 결국 ‘Ether wind’를 증명하지 못했다.
첨언
이는 에테르의 존재를 완벽하게 반증한 실험이고 그 당시에 물리학 실험에서 가장 정밀하게 이뤄진 실험 중에 하나이다. 또한 현재에 이르러서는 2015년 중력파 검출에 성공한 LIGO에서 사용한 실험 기구가 바로 이 간섭형 검출기이다. 기초원리는 마이컬슨-몰리 간섭계와 동일하고 여기에 기술적 정교함을 더해 가장 정밀한 검출기를 만들어냈다.
상대성 이론의 시작과 끝에 마이컬슨-몰리 검출기가 함께 했다고 할 수 있겠다. 중력파나 중력파 검출기에 관심이 있다면 ‘Gravitational waves volume 1’ by M. Maggiore을 찾아보기 바란다.
‘Ether’라는 개념을 되살리기 위해, 또 이러한 실험결과를 설명하기 위한 많은 노력이 있었지만 모든 설명은 에테르가 존재하지 않는다는 결론에 도달했다.
대신에 George F. Fitzgerald 와 Hendrik A. Lorentz는 놀라운 생각을 제안했다. 1890년대에 Fitzgerald와 Lorentz는 임기응변으로 v의 속도로 움직이는 물체는 $\sqrt{1-v^2/c^2}$배만큼 길이가 수축한다고 제안했다. 이 수축 결과는 간섭계 실험에서 Arm의 길이를 수축시켜 경로차가 발생하지 않도록 해주었다.
마이컬슨-몰리 실험의 결과는 매질을 통해 전파되던 기존의 파동과는 다른 개념의 광파가 존재함을 시사하고 높은 속도로 움직이는 관성계에서 Galilean transformation이 성립하지 않는다는 것을 의미했다.
이제 무대는 1905년 등장한 Einstein의 특수 상대성 이론을 위해 세팅 되었다.
1.4 특수 상대성 이론의 두 가지 가정
특수 상대성 이론의 두가지 가정으로 기존의 존재했던 난제를 과감히 해결해 버렸다.
-
The Principle of Relativity: All the laws of physics have the same form in all inertial reference frames.
-
The Constancy of the Speed of Light: The speed of light in vacuum has the same value, $c = 3.0 \times 10^8 m/s$, in all inertial frames, regardless of the velocity of the observer or the velocity of the source emitting the light.
첫 번째 가정은 물리학의 모든 법칙을 바꿔버렸다.
전자기학, 광학, 열역학, 역학 등 모든 물리학 이론은 같은 수학적 방법으로 서술되어야 하고 이를 단어로 등속도로 움직이는 frame 내에서의 covariant라고 한다. 이는 뉴턴의 역학 법칙의 확장이고 일반화이다. Einstein의 상대론적 원칙은 어떠한 실험도 absolute한 frame이 존재하지 않으며 모든 기준 좌표계는 실험에서 구분할 수 없다는 것을 시사한다.
빛의 속도가 불변이라는 두 번째 가정은 첫 번째 가정과 일맥상통한다.
만약 빛의 속도가 관성 좌표계마다 달랐고 하나의 좌표계에서만 c 라는 속력을 가졌다면 하나의 기준 좌표계가 존재할 수밖에 없다. 이제 상대론에서 두 가정의 의미가 같다는 것을 이해할 수 있을 것이다. 에테르의 존재를 완전히 지워버린 두 번째 가정은 모든 관성 좌표계에서 빛의 속도는 c라는 것을 의미한다. 이는 다양한 실험적 방법들로 증명되어 왔다. 아마 가장 직관적인 방법은 진동수가 매우 높은 전자기파(감마선)가 불안정한 입자(neutral pions와 같은)에서 방출될 때 빛의 99.975% 속도로 전파되는 것을 관측하는 것이다. 이 실험으로 진공에서 빛의 속도를 5번째 유효숫자까지 측정할 수 있다.
아마 이제는 Galilean transformations이 틀렸다는 것을 알았을 것이다. 올바른 좌표, 시간 transformation은 모든 물리 법칙에서 covariant를 유지해야 한다. 이를 Lorentz transformations이라고 불린다. 뉴턴의 법칙은 낮은 속도에 제한된 역학 법칙이다.
일반적으로 뉴턴 법칙은 아인슈타인의 역학적 상대론에 포함되며, 모든 속도에 대해서 모든 물리학 법칙을 Lorentz transformation을 통해 적용할 수 있다.
첨언
상대성 이론이라는 전공 과목은 학부 4학년 과목이거나 대학원 과목이다. 연구를 하기 위해서는 분야에 따라 필수적으로 알아야 하지만 요구하는 깊이는 천차만별이라고 들었다. 텐서만 이해할 수 있다면 학부수준에서는 Hartle이나 Schutz의 책을 추천한다. 후반부에 유도 과정이나 다루는 내용이 다르니 둘 다 보면 좋다. 그리고 웃기게도 상대론적 양자역학, 전자기학, 열역학 등이 궁금하다면 각 전공 이름 앞에 relativistic 단어만 붙이면 된다. 한국어 책으로는 상대론적 양자역학이 유일하기 때문에 하나쯤 소장하는 것도 나쁘지 않다.
1.5 특수 상대론으로 인한 현상들
광학 먼저 포스팅 예정



Leave a comment